Lagrange-multiplikator
En Lagrange-multiplikator bruges til at finde ekstrema - dvs. maksimum eller minimum - for en funktion givet en til flere sidebetingelser.[1]
Metoden
redigérkan være en funktion af variable , ... og . Sidebetingelsen kan formuleres som en funktion , der skal være lig med nul:
Funktionen er maksimeret eller minimeret uden sidebetingelse, når gradient er nul:
hvor er nabla-operatoren. Dvs. at alle hældninger mht. alle variable skal være nul.
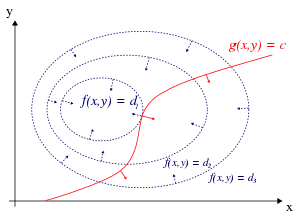
For at indføre sigebetingelsen benyttes det, at de to funktioner skal røre hinanden tangentielt som illustreret i figuren. Da en gradient er vinkelret på en konturlinje. Vil det sige, at de to gradienter skal være parallelle:
hvilket også kan skrives som en proportionalitet:
Dvs. at en ny størrelse kan defineres, hvis gradient skal være nul:
Her er en proportionalitetskonstant kaldet en Lagrange-multiplikator. Denne ligning giver et ligningssystem, som kan løses.[1]
Kildehenvisninger
redigér- ^ a b Blundell, Stephen J.; Blundell, Katherine M. (2006). "C.13 Lagrange multipliers". Concepts in Thermal Physics (engelsk) (1. udgave). Oxford University Press. s. 449-450. ISBN 978-0-19-856770-7.



